Question préliminaire [utile pour la question 4 ci-dessous]
Développer (3x-2)
2 puis (3x-8).(3x-2)
2 (on donnera le résultat sous forme réduite et ordonnée).
-
|
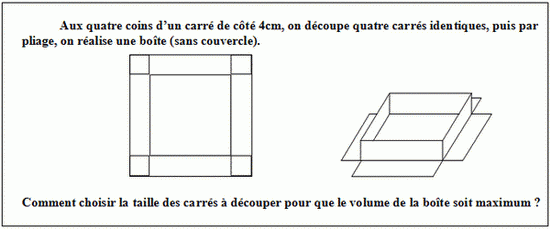
On note
x le côté de chaque carré découpé et
v(x) le volume de la boîte obtenue.
|
1. Dans quel intervalle I le nombre x varie-t-il ?
2. a) Si les carrés découpés sont de 1cm de côté, quel est alors le volume de la boîte ?
En utilisant le langage des fonctions, le résultat peut s'exprimer sous diverses formes telles que (compléter) : v(1) = ........... ou : l'image de .......... par la fonction v est

b) Même question pour x = 0,5 et x = 1,5 .
c) Pour x quelconque dans I, exprimer v(x) en fonction de x .
Rappel : le volume d'un pavé droit de dimensions L, l, h est : V = L* l* h .
|
3. Approche numérique et graphique [calculatrice utilisée : TI 82 , 83 ou 84]
a) Mémoriser la fonction v dans la calculatrice. |
Procédure :
- On accède à l'éditeur de fonctions par la touche
- On fait le ménage (si nécessaire) : si une expression apparaît sur la ligne Y1 = , on l'efface par
 ; on peut aussi utiliser une fonction " libre " Y2 ou Y3… ; on peut aussi utiliser une fonction " libre " Y2 ou Y3…
- On introduit alors la fonction, voir ci-contre.
-
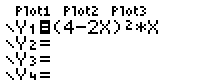
|
|
b) Dresser sur la calculatrice la table de valeurs (approchées) de la fonction v sur l'intervalle [0,2] avec le pas 0,1.
|
Procédure:
- On prépare la table :
 (touches (touches
  ) )
- On dresse la table :
 (on peut s'y déplacer par les touches de curseur (on peut s'y déplacer par les touches de curseur

-

-
|
|
Vérifier la cohérence avec les résultats des questions 2a) et 2b).
En utilisant la table, proposer une conjecture en réponse à la question posée dans l'encadré ci-dessus.
c)Tracer sur la calculatrice une ébauche de la représentation graphique de la fonction v sur l'intervalle [0,2].
|
Procédure
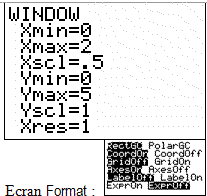
- On règle la fenêtre d'affichage :
- On demande la représentation graphique :

- On peut alors suivre la trace d'un point de la courbe (touche
 et touches de curseur et touches de curseur
 on peut lire les coordonnées du point mobile sur la courbe si la commande "CoordOn" est active dans le menu Format (accessible par la touche [Format] ). on peut lire les coordonnées du point mobile sur la courbe si la commande "CoordOn" est active dans le menu Format (accessible par la touche [Format] ).
-
|
En utilisant l'écran graphique, proposer une conjecture sur le volume maximum de la boîte. Est-elle compatible avec celle énoncée à la question 3b) ?
d) En utilisant de nouveaux choix, soit dans le réglage de la table (
 avec la possibilité d'affiner le pas
 ), soit dans celui de la fenêtre d'affichage (
 ) avec la possibilité de jouer sur Xmin, Xmax, Ymin, Ymax ou bien
 avec l'utilisation de ZBox par exemple), conjecturer un encadrement d'amplitude 10 -3 (ou mieux !) de la longueur x du côté des carrés découpés pour laquelle le volume v(x) de la boîte semble être maximum.
|
Approche algébrique
a) A l'aide de la calculatrice, trouver une valeur approchée de v(
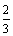 ): on peut utiliser la table, ou bien, dans l'écran de calcul initial, taper Y1(2/3) ( Y1 s'obtient dans
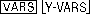 1: Function 1: Y1).
Comparer le résultat à v(0,666), v(0,667), v(0,6666), v(0,6667).
b) Calculer v(
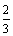 ) à partir de l'expression algébrique de v(x) (on attend ici le résultat exact).
Vérifier que
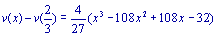
En utilisant la question préliminaire, factoriser la différence v(x) - v(
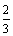 ) et étudier son signe.
Conclure.
|