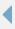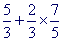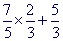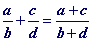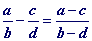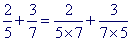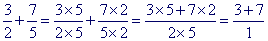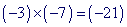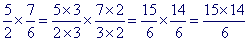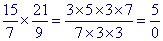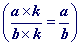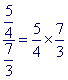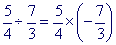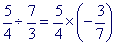| Code |
Description |
Explications |
|
A
|
Priorité
des
calculs
|
Les règles de priorité sont souvent transgressées de par le contexte du calcul. Il est à noter qu'en général ce n'est pas la méconnaissance de ces règles qui entraîne ces erreurs, mais plutôt la reconnaissance dans le calcul d'une forme familière vers laquelle l'élève est " attiré ". Par exemple dans le calcul
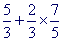 certains élèves, ne voyant que la somme de deux fractions de même dénominateur, seront poussés à effectuer cette opération en priorité sans même se poser la question de savoir si justement c'est cette opération qui est prioritaire.
Il est à noter que les erreurs seront moins fréquentes si le même calcul se présente sous la forme
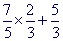 car l'opération prioritaire arrive en première position dans la lecture du calcul.
|
|
B
|
Règles
d'addition et
de
soustraction
de deux
fractions
|
Les règles d'addition et de soustraction de deux fractions ont été la plupart du temps " déformées " voire " réinventées ". Souvent les élèves étant confrontés à la somme de deux fractions ont essayé de s'en sortir en inventant des règles du type :
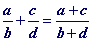 ou
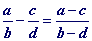 .
Certains ont tout de même pris la peine de réduire les fractions au même dénominateur mais ont tout de même appliqué les deux non-règles ci-dessus. Ceci peut s'expliquer soit par un besoin d'avancer dans le calcul coûte que coûte ou alors par analogie faite entre les règles d'addition et de soustraction et celle de la multiplication de deux fractions ce qui dans les deux cas a conduit les élèves à utiliser les deux non-règles précédemment citées.
|
|
C
|
Mise
au
même
dénominateur.
|
Certains élèves ont fait des mises au même dénominateur erronées car ils n'ont pas respecté la règle d'égalité des fractions. Par exemple ils ont écrit :
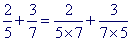 . Il est vrai que pour eux l'objectif est atteint et ils ne se soucient pas de la validité de la transformation opérée. On peut se demander si cette transformation n'est pas la seule préoccupation de l'élève à ce moment-là, déconnecté alors de toute rationalité mathématique.
|
|
D
|
Simplification
d'une somme
ou d'une
différence.
|
Cette erreur relève d'une analogie faite avec la simplification d'un produit de fractions. Dans ce cas, les élèves ont acquis des méthodes qui pour eux ne relèvent plus de règles à proprement parler ou du moins dont ils ont oublié les champs d'applications. Par exemple, ils ont écrit :
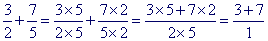 .
|
|
E
|
Addition de
nombres
relatifs
|
Une erreur fréquente se produit lors de l'addition de deux nombres négatifs. Par exemple les élèves écrivent -3-2 = -1. Cette erreur est due au fait que le second signe "-" est considéré comme un signe opératoire et que pour les élèves c'est la seule opération qui est à faire dans ce calcul, ce qui jusque là ne peut pas être considéré comme faux, par contre ils occultent complètement le premier signe et ne s'en préoccupent qu'une fois l'opération effectuée. Ils retournent en fait ici dans un monde bien maîtrisé qui est celui de la différence de deux entiers naturels dont le premier est plus grand que le second. Effectivement, il y a ici un phénomène d'attirance comme dans l'erreur A vers cette forme bien connue, au détriment de tous les autres concepts enseignés depuis.
Il est vrai que les mêmes élèves ne font pas toujours l'erreur sur le calcul car ici le calcul "-2-5" ne donne pas un résultat positif et doit sûrement replonger l'élève dans le monde des entiers relatifs. De plus il est alors confronté à quelque chose du type "- -3" qui l'amène à se poser des questions sur la validité de ce qu'il vient de faire et le conduit donc à reconsidérer le calcul car il n'est pas habitué à traiter des formes du type "- -3".
|
|
F
|
Analogie
entre la règle
de
multiplication
de deux
nombres
relatifs et
celle
d'addition.
|

Certains élèves ont pris l'habitude de compter le nombre de facteurs négatifs dans un produit ou un quotient de plusieurs nombres relatifs et extrapolent ceci sur l'addition de deux nombres relatifs. Par exemple : -2-7
devient 9 car ils appliquent la règle d'addition de fractions en ce qui concerne les distances à zéro et la règle de multiplication pour le signe de la somme.
|
|
G
|
Règle du
produit de
deux nombres
relatifs.
|
Les erreurs constatées ici sont principalement sur le signe du produit. Peut-être la confusion inverse de l'erreur du type F se fait ici, les élèves utilisant la règle d'addition de deux nombres relatifs pour donner le signe d'un produit. Par exemple
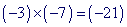 .
|
|
H
|
Mise au
même
dénominateur
pour un
produit
|
Ici encore, l'élève réagit à une forme et fait une action sans y accoler un but précis, ou du moins sans objectif à long terme. Sa seule volonté ici est de réduire les deux fractions au même dénominateur sans se demander pourquoi il doit faire ceci. Cette action qui n'est pas une erreur en soit au départ mais seulement une maladresse se transforme ensuite en erreur car, dans la majorité des cas, ceux-ci font une analogie avec la règle d'addition de deux fractions et ne multiplient pas les dénominateurs entre eux. Par exemple :
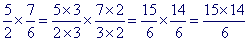 .
Il est vrai que cette erreur arrive plus fréquemment lorsque l'un des dénominateurs est un multiple de l'autre mais pas de façon flagrante. On peut supposer encore qu'il y a une certaine attirance vers une action que l'on sait faire car l'on a reconnu une forme familière.
Par contre quelques rares élèves, même après avoir réduit les deux fractions au même dénominateur, utilisent correctement la règle du produit mais au prix de calculs souvent compliqués.
|
|
I
|
Reste 0 après
une
simplification.
|
Lorsque des élèves simplifient une fraction ou un produit de fractions avant d'effectuer celui-ci, il arrive parfois que tous les facteurs du numérateur ou du dénominateur (ou des deux) se simplifient. Quelques élèves écrivent alors 0 à la place du produit. Par exemple :
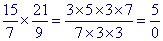 . Cette erreur relève sûrement du fait qu'à force de simplifier, ils perdent le sens de ce qu'ils font et que pour eux il s'agit juste de barrer les nombres égaux au numérateur et au dénominateur sans avoir en tête qu'ils utilisent la règle
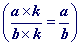 et que tout nombre
a s'écrit
1xa. Ils focalisent ce travail sur les symboles et " barrer " revient alors à faire disparaître l'écriture du nombre.
|
|
J
|
Règle du
quotient de
deux fractions
|
Il s'agit là en général d'une méconnaissance de la règle nouvellement enseignée en quatrième et qui donne lieu à diverses tentatives erronées pour effectuer le calcul. Par exemple :
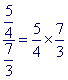 .
Ici, si le premier calcul avait été écrit avec le signe
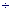 , l'erreur n'aurait sûrement pas été commise car les formes obtenues auraient été trop proches.
|
|
K
|
Confusion
entre inverse
et opposé
|
Ces élèves ont confondu l'inverse d'un nombre soit avec son opposé, soit avec l'opposé de son inverse bien que la règle du quotient soit connue. Par exemple
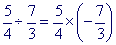 ou encore .....
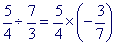 .
|

 RECHERCHE
RECHERCHE